A cellular automaton (plural cellular automata, abbrev. CA) is a discrete model of computation that have found application in various areas, including physics, biology, chemistry, traffic flow, ecology, generative art and music, and many others. In this two-part series we are going to explore how to simulate a evacuation process using a two-dimensional CA.
In this first part we will give a quick overview of what a CA is, discuss our implementation strategy and then take a look at the python code.
In the second part, we will setup some experiments, run the simulations using the multiprocessing module and draw some conclusions based on the results. Also, pygame will help us to visualize the simulations. Let’s do it!
In this image, we have a neural network with one layer and 3 neurons. The neural network gets the data from the input layer and transforms the data according to the structure defined.
Each of these arrows and neurons represents an operation in the network. Usually, these operations are multiplication and sum between the data and weights.
These weights are calculated using an optimization algorithm called backpropagation. Backpropagation is a method that exploits the chain rule of calculus to obtain the best neural network weights.
In this article, we will optimize our neural network without backpropagation. Instead, we will apply a bio-inspired algorithm Particle Swarm Optimization.
Cellular Automata — brief overview
A cellular automaton consists of a regular grid of cells, such that each cell can be in one of a finite number of states, and the grid itself can be in any finite number of dimensions.
For each cell, a set of cells called its neighborhood is defined relative to the specified cell. An initial state (time t = 0) is selected by assigning a state for each cell.
A new generation is created (advancing t by 1), according to some update rule that determines the new state of each cell in terms of the current state of the cell and the states of the cells in its neighborhood.
The rule for updating the state of cells can be either deterministic or based on some probability distribution, and in most cases, it stays the same for the entire simulation.
If the update rule is not deterministic, we have a stochastic cellular automaton. The order in which the update rule is applied is extremely important, and is most cases it is applied to the whole grid simultaneously, which is known as a parallel or synchronous update.
In this case, the state of every cell in the model is updated together, before any of the new states influence other cells. Every cell at step t+1 sees the same “frozen picture” of the grid state at the previous step t.
In contrast, an asynchronous update is able to update individual cells independently, in such a way that the new state of a cell can immediately affect the calculation of states in its neighbouring cells. It is important not to confuse update rule with update order.
The update rule is the function that takes as input the current cell state and the current cell neighborhood, and outputs a new state to update the current cell. The update order is just the cell order in which this function is applied (synchronously or using some asynchronous strategy).
Given two identical CAs (having the same dimension, update rule and initial state), the choice of a synchronous or asynchronous update, in most cases, will produce a completely different CA behavior.
Which one to choose will depend on the simulation goals and assumptions. The synchronous approach assumes the presence of a global clock to ensure all cells are updated together. While convenient for some systems, this might be an unrealistic assumption if the model is intended to represent, for example, a living system where there is no evidence of the presence of such a device.
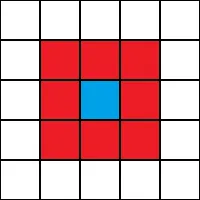
Another point of attention when implementing a CA is what happens at the boundaries of the grid. If, for example, we are using a Moore neighborhood, what is the neighborhood for cells at the edges?
One way to solve this is to let these cells have a constant state. Another method is to define neighborhoods differently for these cells. As in the case of the update order, the method chosen will affect the CA behavior.
Cellular automata is a huge topic, with plenty of books and papers on the subject. If you are new to CAs, a good starting point is the Wikipedia article and this Stanford page on the subject.
CA evacuation model
The obvious choice here is a 2D CA, which represents a room where each cell can be either empty, occupied by a person, occupied by an obstacle, or be an exit cell. He have just defined the set of possible states for a cell and the dimension of our CA. Now comes the hard part: how to define the update rule and update order?
Since we are dealing with people moving inside a room, by “update rule” we really mean, how people move in respect to each other and possible obstacles? Let’s first start with the easier rules, which are very suitable for our simulation purposes:
- Obstacle cells never change their state and cannot be occupied.
- Exit cells never change their state.
- Each empty or exit cell can be occupied by at most one individual.
The rules for the actual motion of people are a bit more involved and depend on the update order chosen. For our simulation we are going to use a parallel (aka synchronous) update rule.
This means that at very iteration, people may try to move to the same location, which goes against rule 3 above. To solve this, we will resolve these conflicts in a clever way.
Now, how do people choose their move? In an evacuation situation, the goal is always the closest exit. So our move algorithm for a person occupying cell C is as follows:

In other words, we look around the current cell and choose only the cells that we can move to (empty ones or some exit) that are closer or at a equal distance to some exit than the cell we currently are.
Then we just choose the move that gets us closest to some exit. What this means is that people will try to move to a better spot if they can, but will also try to move even when their distance to some exit stays the same with the movement. Movements that get a person farther away from some exit are never considered.
To calculate the distance cost from cell A to the nearest exit E we should take obstacles into account. The Dijkstra algorithm will handle that for us. Each cell will have an associated cost value indicating how farther away it is from the nearest exit. This map is sometimes called a floor field.
Two things are important to note: first, diagonal movements have a cost of 2, horizontal or vertical movements cost 1. Second, we are not considering people as obstacles.
That would be like solving an ever-changing maze, which makes no sense. More importantly, this allows us to calculate a Dijkstra map once and reuse it for the entire simulation!
One could argue that when choosing an exit, the congestion around the exits is an important factor. This is certainly true, it’s a kind of a dilemma: do I go for the nearest exit, which is crowded, or do I go towards some farther away exit, which is less crowded?
There are plenty of papers that implement this behavior, but in our model we choose not to to keep it simple. For example, in this paper they use parameter α (in the range [0, 1]) which reflects the degree of impatience of people during the evacuation.
When α = 0 only the distance factor is considered, when α = 1 only congestion is considered, and for 0 < α < 1, these factors are weighted in order to choose a target exit. Let’s recap our rules of movement:
- Obstacle cells never change their state and cannot be occupied.
- Exit cells never change their state.
- Each empty or exit cell can be occupied by at most one individual.
- People will try to move to the nearest empty cell that is closer or at a equal distance from some exit than the cell they currently are.
- If there is no available cell that fits the rules above, no movement will take place.
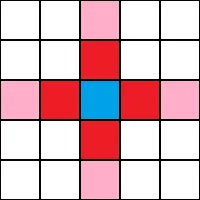
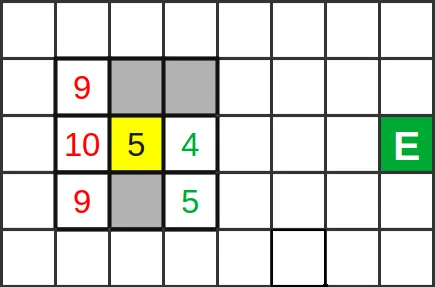
Let’s analyze two cases below. In both figures we see a yellow cell and its moore neighborhood. Grey cells are obstacles and E marks the exit. Cells with number are empty and free to move.
Suppose the yellow cell is the current cell and there is an individual there trying to move. The numbers are the distance to the exit, and we see that only the values marked in green are less than or equal to 5. In this case, the cell marked with 4 is the best move.
In Figure 2 we see another situation. The red cross is occupied by another person, we cannot move there. In this case the green cell marked with 5, despite not improving our distance towards the exit, will be chosen.
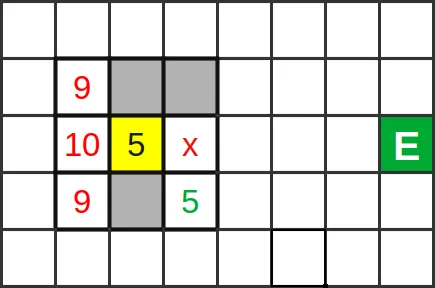
One thing is missing in our implementation: how do we handle conflicts?Since we are doing a parallel update, more than one individual might try to move to the same empty cell.
To resolve this, we simply don’t perform the move right away, instead we keep the “candidate moves” for all cells in a dictionary.
After all candidate moves have been parsed, we iterate this dictionary, and if there is more than one candidate for a cell, we simply randomly choose one that will be eligible to move, and update the grid accordingly.
Right now, our only source of randomness is the way in which we solve move conflicts. To make things a little bit more realistic let’s add a variable called panic_prob, which represents the probability that a person will not move, even if they can.
We could model this variable by drawing from a Beta distribution, so that each person would have its own panic probability, but to simplify things, we will just set it to a constant value. We have all the information we need to implement this, so let’s code!
Click: CA evacuation model code
First, we define a CACell class to represent our cell state. Notice that besides the state, we also have a variable called properties, which we’ll use to add some properties to the cell (like panic probability, for example).
Then we define the CARoom class, which contains all our simulation logic. We define the room dimensions and set each cell to be a square of size 0.4m.
As each cell can be occupied by a at most one person, this is the value most used in the literature, giving a density of approximately 6 persons per m2. We also allocate space for our cells, create a reference to the exit cells and initialize the dijkstra map to None.
Besides the usual get and set stuff, we have some interesting methods. The get_graph method loops through the cells and connects the empty ones, setting their squared distance as the connection weight (the real distance does not matter).
The get_dijkistra_map method uses the graph generated in get_graph and Dijkstra’s algorithm to assign a cost to every empty cell, representing the distance towards the nearest exit.
The step_parallel method is where things happen. It represents a single step of the simulation. We basically loop through each cell and when we find a cell with the state CACell.PERSON_STATE, we try to move to the nearest empty cell that will get us closer to the nearest exit, as explained in the previous section.
Notice that before moving, we flip a coin to check for a panic situation, in which case there is no movement. Also, notice that all moves are stored in a variable called new_state, indexed by the cell.
We later iterate new_state and resolve every cell that has two or more candidate moves, picking one at random. Finally, while resolving these conflicts, we also remove from the simulation every person that has reached an exit cell and return the total number of evacuees in this step.
We end part 1 of this series testing what we have done so far: we create a simple 10m x 10m room with external walls, a centered square-shaped obstacle and a single exit. Then for each empty cell, we add a person with a probability given by full_factor. Then we call step_parallel until everyone is evacuated.
Notice that since each cell is a 0.4m x 0.4m square and we have external walls and a 4 x 4 cells obstacle, there is room for approximately 23 * 23 -16 = 513 people. Given a full_factor of 0.3, we have an expected value of ~154 evacuees. We also implemented a simple __str__ method, so that you can see what is happening in the console.
Our Dijkstra implementation is very short:

To run everything, just add CA.py and dijkstra.py to the same folder and type in:
python3 CA.py
In part 2 we are going to setup some experiments and run them using the multiprocessing module, to speed things up. Also, it is important to be able to visualize the simulations, so pygame will help us with that. See you later!